|
I. Introduction
The homogeneous broadening of the vibrational Raman bands of liquids and gases is due to a number of stochastic processes such as molecular re-orientation, vibrational energy transfer, translational diffusion, and shape fluctuations of the molecular polarizibility ellipsoid. The bandshapes can be expressed in terms of the correlation functions characterizing these processes which are in turn closely related to the structure of the particular liquid (or gas). Even a limited knowledge of the correlation functions therefore represents a valuable check for any hypothetical model of the liquid (or gas) structure.
Although the relation between the correlation functions and the Raman bandshapes has been extensively studied [1-5], the problem of its practical exploitation is still far from being solved. The main obstacles on the way to the evaluation of experimental bandshapes in terms of correlation functions are a) the mixing of the contributions due to qualitatively different homogeneous broadening mechanisms and b) the presence of the heterogeneous (adiabatic) vibrational frequency shifts.
In this paper I propose a simple evaluation method which enables one to determine the re-orientation correlation function regardless of the presence of other broadening processes (both homogeneous and heterogeneous). The presentation of the method requires a short resumé of the theory of Raman bandshapes. I will use this occasion to state, in a form as compact as possible, all the assumptions and approximations it involves (this, I hope, might prompt others to attack its limits).
The electric component of the excitation beam can be written as
| |
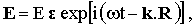
| (1) |
where R is the position vector and ε, k and ω are the unit polarization vector, the wave vector, and the frequency of the beam, respectively.
Consider now a molecule located at R (its dimensions are supposed to be negligible with respect to the wavelength of the incident light). Assuming the vibration-rotation interactions to be small, we are allowed to speak about the vibrational transition elements Ars of the polarizibility tensor A (the indices r and s refer to the particular vibrational states). The vibrational Raman band can now be interpreted as the secondary emission due to the component Drs of the induced dipole moment (for the basic theory of Raman effect, see ref.[6]):
| |
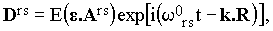
| (2) |
where ωors = ωe - ωrs, with ωrs being the circular frequency of the vibrational transition from r to s.
The electric component of the radiative electromagnetic field of Drs at a distance r from the molecule is given [7] by:
| |
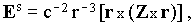
| (3) |
where | |
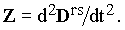
| (4) |
|
If the scattered light is passed through a polarizer, then the electric field vector beyond the polarizer is
| |
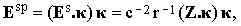
| (5) |
where κ is the unit vector defining the orientation of the polarizer. The vector Drs can be expressed as a Fourier integral with the density distribution
| |
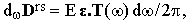
| (6) |
where | |
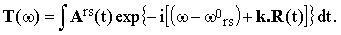
| (7) |
The Fourier densities of Z and Esp can be easily obtained using Eqs.(4) and (5):
| |
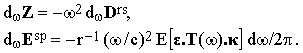
| (8) |
The intensity scattered within a frequency interval dω and a solid angle element dΩ is therefore
| |
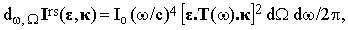
| (9) |
where Io = cE2/2π is the intensity of the incident beam. The differential cross-section of this process is then
| |
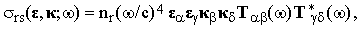
| (10) |
where nr is the probability of finding the molecule in the r-th vibrational state (at this point we start using the summation convention for the Greek indices).
| |
Eq.(10) refers to a single molecule; in order to obtain practical results we must carry out the ensemble averaging (this will be denoted by the <...> brackets). The result is
| |
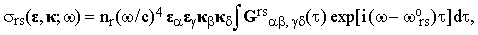
| (11) |
where
| |
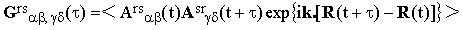
| (12) |
is the correlation tensor.
A real excitation beam is composed of two components of the form (1) with frequencies ω and -ω, respectively. If the width of the band is very small in comparison with ωors then, by Eq.(11), the contribution of the component with frequency -ω to σrs is negligible. The (-ω) component will however contribute to the σrs scattering so that the total cross section for a real beam is
| |
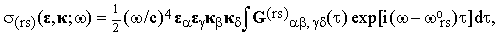
| (13) |
where
| |
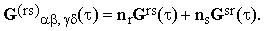
| (14) |
For simplicity, we will limit ourselves to the case ns<<nr. This, of course, does not represent any loss of generality since the final results do not change when the restriction is dropped.
Eqs.(11) and (13) should be compared with the slightly less general formula given by Gordon [5]. The most serious objection to their validity arises from the assumption of zero vibration-rotation interaction. It should be noticed, however, that the VR interactions affect mainly the antisymmetric component of the band. Their neglecting therefore affects predominantly the complex part of Grs while the real part (which is strongly dominant in most practical cases) remains much more reliable.
| |
The 81 components of Grs are interconnected by a number of symmetry requirements. First of all, Ars is a symmetric tensor so that the components Grsαβ,γδ must be invariant with respect to the permutations of the indices α,β and γ,δ (this leaves us with 36 independent components). The most significant reduction arises from the assumption of the isotropy of the sample. As an ensemble-averaged quantity, the tensor Grs(τ) must respect the macroscopic symmetry of the ensemble. Its components therefore have to be invariant with respect to any mirror reflection in a coordinate plane (this leaves only 21 components different from zero) as well as with respect to any permutation of the coordinate axes. This means that among the 21 non-zero components, at most three can be mutually independent; a possible choice of the three is GrsXX,XX, GrsXX,YY, and GrsXY,XY. But the required isotropy implies invariance with respect to any rotation of the coordinate system. Applying a π/4 rotation about the Z-axis to GrsXX,XX we deduce that
| |
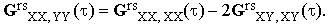
| (15) |
For an isotropic sample the tensor Grs has therefore just two independent components. A convenient choice of the two is GrsXX,XX and GrsXY,XY since these parameters are directly related to conventional experiments. An easy transformation of Eq.(13) gives
| |
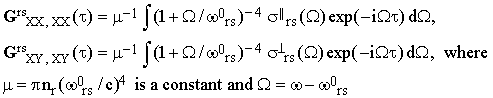
| (16) |
is the angular frequency referred to the center of the band as its origin.
| |
|
II. Factorization of the correlation tensor.
a) Vibrational energy transfer
When the vibration-rotation interaction is weak than the averaging over the vibrational degrees of freeedom may be carried out separately. In this case a transition terminating the existence of the molecule in any of the vibrational states r and s at the moment T is taken care by putting Ars(t)=0 for t>T. The result of the partial averaging is
| |

| (17) |
where the ensemble average is now taken over all degrees of freedom except the vibrational ones. The reduced correlation function Vi(τ) can be interpreted as the Fourier transform of the normalized density profile of the i-th vibrational energy level corrected for the heterogeneous vibrational energy shifts. Phenomenologically, it can be approximated by the formula
| |
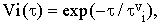
| (18) |
where τvi is the mean lifetime of the molecule in the i-th vibrational state.
| |
The effectiveness of the vibrational energy transfer as a broadening mechanism increases rapidly with the size of the molecule because of the increasing density of its vibrational states. On the other hand, the molecular re-orientation contribution tends to decrease with increasing molecular dimensions. For sufficiently large molecules, the re-orientation can be therefore just a secondary effect, although it has been shown [2] to be dominant in the case of several small molecules.
b) Translational diffusion
The exponential term in Eq.(12) includes the effects of the translational diffusion of molecules over distances comparable with the wavelength of the incident light. Since the long-range diffusion can hardly be correlated with the local processes governing the behaviour of Ars, Eq.(17) may be written as
| |
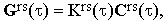
| (19) |
where
| |
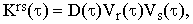
| (20) |
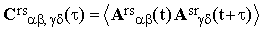
| (21) |
and
| |
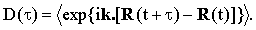
| (22) |
In low-density gases, where the translational diffusion reduces to the free translation, Eq.(22) leads straightforwardly to the standard formulas for Doppler broadening. In dense gases and liquids the translational motions are severely limited and D(τ) is expected to be almost indistinguishable from unity.
c) Reorientation and shape-fluctuations of Ars
When expressed in the molecular-frame coordinates (defined by the main axes of the tensor of inertia), Ars(t) can be written as
| |
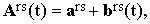
| (23) |
where ars is the average value of Ars(t) and brs(t) is the stochastic intermolecular contribution including the shape deformations of Ars. Transformed to laboratory coordinates, Eq.(23) becomes
| |
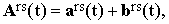
| (24) |
where the time dependence of ars(t) is determined exclusively by the re-orientation process.
The importance of the second term in Eq.(24) is a great question mark. Since it does not appear anywhere in the theoretical literature, we might apply the Occam's razor rule and neglect it until its importance will be demonstrated experimentally. Before doing so, however, I would like to formulate a little bit more realistic criterion for the validity of such an approximation.
The tensor brs can be interpreted also as the response of the molecular polarizibility to the fluctuating electric field e(t) generated by the surrounding molecules. Hence
| |
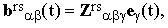
| (25) |
where Zrs is the transition hyper-polarizibility tensor which figures also in the theory of hyper-Raman effect (the scattering at twice the excitation frequency). Given the polarization vectors ε and κ, it is easy to show that
| |
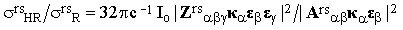
| (26) |
where Io is the intensity of the incident beam and σrsR and σrsHR are the experimentally accessible Raman and hyper-Raman scattering cross-sections, respectively. The term brs(t) is therefore negligible with respect to ars if
| |
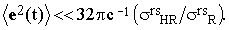
| (27) |
Assuming the validity of this condition, Eq.(21) reduces to
| |
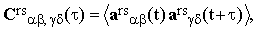
| (28) |
where the averaging regards only the rotational degrees of freedom.
In order to avoid any possible misunderstanding, I would like to underline that the preceding discussion does not involve any attempt to separate one from the other those relaxation processes which influence the orientation of the molecule. The tensor Crs(τ) therefore still includes, for example, the combined effects of the intermolecular rotation-rotation and rotation-translation interactions. As a matter of fact, the mutual separation of thy various mechanisms promoting the molecular re-orientation can not be achieved by any method based exclusively on Raman scattering. A relevant information of this kind can be deduced only from the comparison of the experimentally determined tensor Crs(τ) with the correlation tensor calculated from an appropriate model.
| |
|
III. Symmetry properties of the correlation tensor.
Decomposing ars(t) in the standard way into its scalar and traceless components,
| |
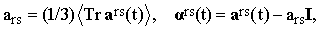
| (29) |
Crs(τ) assumes the form
| |
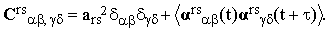
| (30) |
In the isotropic case the re-orientation of any traceless tensor α can be described in terms of a single correlation function g(τ). This is a direct consequence of the relation
| |
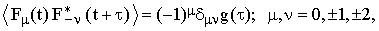
| (31) |
where Fμ are the spherical components of α defined as [8]
| |
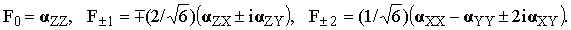
| (32) |
Introducing the reduced correlation function
| |
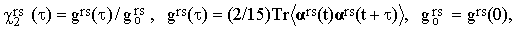
| (33) |
and playing with Eqs.(31) and (32), one can prove that
| |
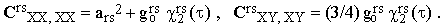
| (34) |
|
IV. Determination of χ(τ) from experimental data.
The reduced correlation function χ2rs(τ) represents a very important piece of information. In order to extract it from the experimental data, let us first define the quantity
| |
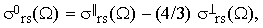
| (35) |
and the normalized bandshape functions
| |
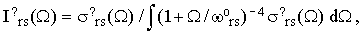
| (36) |
where ? is either "o" or "⊥". Notice that Iors and I⊥rs are easily accessible experimentally since they do not require any absolute intensity measurements. Combining Eqs.(16), (19) and (34) we finally obtain
| |
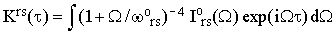
| (37a) |
and
| |
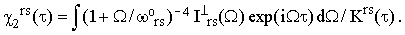
| (37b) |
Equations (37) represent the essence of this paper. When the perpendicular band is not symmetry-forbidden, and the assumptions discussed in the preceding Sections are satisfied, then the separation of χ(τ) from the rest of the homogeneous broadening factors can be achieved without a reference to anything but the experimental bandshapes.
A by-product of this determination is the function Krs(τ) which might be used in combination with infrared data. Let Jrs(Ω) be the normalized shape of the infrared band r→s. Then it is easy to show that, since the scalar broadening processes are common for Raman and IR,
| |
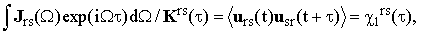
| (38) |
where urs(t) is the unit vector parallel to the corresponding matrix element of the molecular dipole-moment (for a more detailed discussion of the IR correlation functions see reference [5]).
| |
|
V. Inhomogeneous vibrational frequency shifts.
So far we have been considering the vibrational frequency ωors as a dispersionless number. Now we have to face the fact that in condensed phases the adiabatic frequency shifts may often be comparable with other broadening mechanisms [4].
The adiabatic broadening can be conveniently expressed by means of the convolution integral
| |
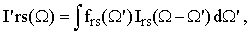
| (39) |
where frs(Ω) is the normalized density distribution of the vibrational frequency ωors and Irs(Ω) is the bandshape function in the absence of the adiabatic frequency shifts.
Substituting Iors and I⊥rs in Eqs.(37) by the real bandshape functions I'ors and I'⊥rs and using the well known theorem on the Fourier transform of a convolution integral, we obtain
| |
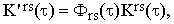
| (40a) |
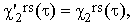
| (40b) |
where
| |
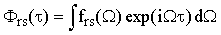
| (41) |
and the apostrophe over a quantity indicates that it is based on the uncorrected experimental bandshapes. Since the function frs(Ω) is the same in Raman and IR, Eq.(38) gives
| |
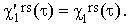
| (42) |
The insensitivity of the vector and tensor re-orientation functions is an extremely important property of the evaluation method discussed in the preceding Section.
The correlation function K'rs(τ) can be interpreted in an interesting way. Expressing frs(Ω) as a convolution of the density profiles of the two vibrational energy levels r and s, it can be shown (see Eq.20) that
| |
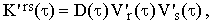
| (43) |
where V'i(τ) is now the Fourier transform of the real density profile (including both homogeneous and inhomogeneous broadening) density profile of the i-th vibrational energy level.
| |
|
VI. Errors in the determination of the center of the band.
The determination of the center-of-the-band frequency ωors is often subjected to considerable experimental error. Let us suppose that an error Δ had been committed which produces an equal shift of the frequency scale Ω. Then, denoting the apparent quantities obtained from Eqs.(37) by a quatation mark, we obtain
| |
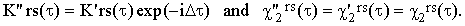
| (44) |
The correlation function χ2rs is therefore unaffected by this type of error while K'rs is multiplied by a somewhat arbitrary oscillatory factor.
Combining Eqs.(37a) and (38), one can determine also the apparent value of χ1rs :
| |
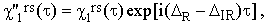
| (45) |
where ΔR and ΔIR are the center-of-the-band errors for the Raman and IR bands, respectively. This result belittles somewhat the importance of Eq.(38) since the technical condition ΔR = ΔIR is very difficult to meet.
| |
|
VII. Conclusions and final comments.
The determination of the correlation function χ2rs(τ) can be carried out with any vibrational band. As has been shown above, the broadening (or splitting) of the band due to weak inter- and intra-molecular interactions does not invalidate the results. Moreover, the method is insensitive to the errors in the center-of-the-band estimation.
When the molecule undergoes internal rotations then there arise four possibilities:
1) The band belongs to a single conformational isomer so that χ2rs(τ) describes the re-orientation properties of this particular species.
2) The band is a localized vibration of a rigid molecular fragment. The function χ2rs(τ) then refers to the re-orientation of this single fragment (an inviting possibility, especially in connection with the study of large molecules and polymers).
3) The band is a heterogeneous mixture of several bands belonging to different conformers. In this case, nothing can be done, unless the transition polarizibility tensors are nearly identical.
4) The band belongs to a long-range torsional motion. In this case the vibration-rotation interaction is usually very strong and makes the results unreliable.
An interesting question is whether the Raman data can possibly provide enough information for an exhaustive characterization of the tensor re-orientation processes in a given sample. Since traceless symmetrical tensors form a five-dimensional linear manifold, let us choose a set of five tensors Wi (i=1,2,...,5) fixed with respect to the molecular frame and orthonormalized under the trace metric ρ(Wi,Wj) = Tr(WiWj). Then any tensor α can be written as a linear combination of Wi's with the coefficients depending only on the geometry of α and any tensor correlation function can be expressed as a linear combination of the 15 independent complex-valued functions χij(τ)=<Tr Wi(t)Wj(t+τ)>.
In practice, it is nearly impossible to find a molecule with 15 different non-overlapping vibrational bands suitable for the re-orientation analysis. However, the situation is substantially better for highly symmetric molecules where the basic set of independent correlation functions is much smaller.
There exists an extensive literature dealing with the interpretation of the re-orientation correlation functions in terms of various liquid (or gas) structure parameters. One of the most general schemes is, for example, the continuous anisotropic diffusion model [9-11] based on a single rotational diffusion tensor as a parameter. The relations between various correlation functions and other properties resulting from any particular model of molecular motion may be quite helpful in a systematic evaluation of Raman data; this problem, however, exceeds the scope of this paper.
| |
References
- 1. R.G.Gordon, J.Chem.Phys. 42,3658 (1965).
- 2. R.G.Gordon, J.Chem.Phys. 43,1307 (1965).
- 3. R.G.Gordon, J.Chem.Phys. 44,1830 (1966).
- 4. R.G.Gordon, J.Chem.Phys. 44,3083 (1966).
- 5. R.G.Gordon, Adv.Magn.Resonance 3,1 (1968).
- 6. G.Placzek,B.Teller, Z.Physik 81,209 (1933).
- 7. W.Heitler, The Quantum Theory of Radiation, Clarendon Press, Oxford, England (1957).
- 8. L.D.Landau, E.M.Lifshitz, Quantum Mechanics, Chapter XIV, Addison-Wesley, Reading,Mass. (1965).
- 9. W.H.Furry, Phys.Rev. 107,7 (1934).
- 10. F.Perrin, J.Phys.Radium 5,497 (1957);7,1 (1936).
- 11. L.D.Favro, Phys.Rev. 119,53 (1960).
|
Acknowledgement:
This research was supported by the National Science Foundation and by the U.S.Office for Naval Research.
|