|
I. Introduction
In this Note we will analyze the finite sums
(1) 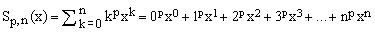
for p = 0, 1, 2, 3,.... and real x (see Section IV for extensions).
These can be considered as the partial sums of the power series whose generic term is kpxk. Using elementary convergence criteria it can be easily shown that the series converges for any real or complex x with modulus smaller than 1. The finite partial sums, however, are well defined for any value of x.
For p = 0, expression (1) this reduces to the truncated geometric series for which
(2) 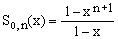
The singularity at x = 1 is only apparent since the nominator in Eq.(2) also has a root at x = 1.
It is instructive to notice that
(3) 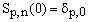 , ,
where the δ symbol is equal to 1 for p = 0 and to 0 otherwise.
This shows that p = 0 is a special case and anticipates the fact that some of the formulae have a different form for p = 0 and p > 0.
In the next Section we will prove that for p > 0 the sums of Eq.(1) can be cast into the form
(4) 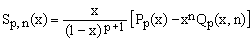 , ,
where Pp(x) is a polynomial in x of order (p-1) and Qp(x,n) is a polynomial of order p in both x and n. Since the finite sum of Eq.(1) is well behaved even for x = 1, the term in the square brackets in Eq.(4) must have at x = 1 a root of multiplicity (p+1).
When x < 1, the limit of Sp,n(x) for n growing to infinity exists and, according to Eq.(4), the sum of the resulting power series is
(5) 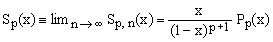 . .
This means that, under the same convergence conditions,
(6) 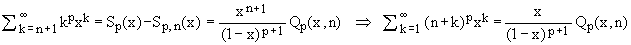
which, apart from a pleasing analogy with Eq.(5), confers a more direct meaning to the bi-polynomials Qp(x,n).
By definition, Sp,0(x) = 0 for any p > 0 and any x. It follows that
(7) 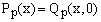 , ,
a relation which can be used as a check.
The purpose of this Note is to prove Eq.(4), derive formulas for the polynomials Pp(x) and Qp(x,n), analyze some of their properties, and tabulate them for a few values of p.
II. Proof of the explicit summation formula
An elementary inspection of Eq.(1) shows the validity of the following recurrence, valid for any p and any finite n
(8) 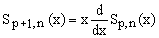 . .
For p = 0 this gives
(9) 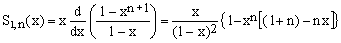 , ,
thus confirming the validity of Eq.(4) for p = 1, with
(10) 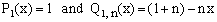 . .
We shall now prove that the validity of Eq.(4) for some p > 0 implies its validity for (p+1).
From Eq.(6) we have
(11) 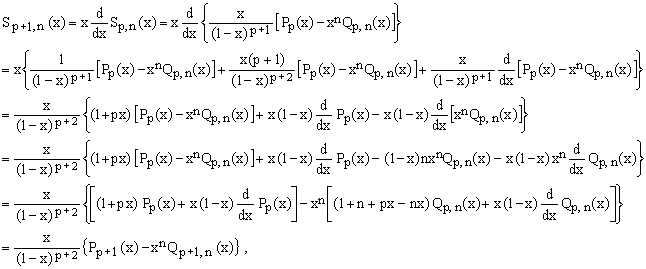
where
(12) 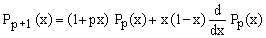
and
(13) 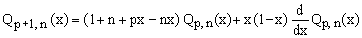 . .
From Eq.(10) it is clear that when Pp(x) is a polynomial of degree (p-1) than Pp+1(x) is indeed a polynomial of degree p. Likewise, Eq.(11) shows that if Qp(x,n) is a polynomial of degree p in x and n, then Qp+1(x,n) is a polynomial of degree (p+1) in both x and n. QED.
III. Determination of the polynomial coefficients
a) The infinite series polynomials Pp(x)
Writing
(14) 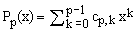 , ,
equation (12) gives the following recurrence for the coefficients
(15)  . .
The coefficients turn out to possess the following symmetry property
(16) 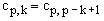 , ,
which can be easily proved by recurrence using Eq.(15) and the fact that it is trivial for p = 1.
TABLE of the first ten polynomials Pp(x)
| k = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p |
| x | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
| 1 |
1 | | | | | | | | | |
| 2 |
1 | 1 | | | | | | | | |
| 3 |
1 | 4 | 1 | | | | | | | |
| 4 |
1 | 11 | 11 | 1 | | | | | | |
| 5 |
1 | 26 | 66 | 26 | 1 | | | | | |
| 6 |
1 | 57 | 302 | 302 | 57 | 1 | | | | |
| 7 |
1 | 120 | 1191 | 2416 | 1191 | 120 | 1 | | | |
| 8 |
1 | 247 | 4293 | 15619 | 15619 | 4293 | 247 | 1 | | |
| 9 |
1 | 509 | 14608 | 88234 | 156190 | 88234 | 14608 | 509 | 1 | |
| 10 |
1 | 1013 | 47840 | 455192 | 1310354 | 1310354 | 455192 | 47840 | 1013 | 1 |
Note added on 15 March 2012: At the time of the writing I needed the finite sums and missed the connection between Sp(x) and the polylogarithms Li-p(x), and hence that the coefficients of Pp(x) are the Eulerian numbers [4], listed as OEIS A008292. My Eq.(5) in fact matches expression (6) for the polylogarithm Li-p(x) in ref.[4].
Consulting the Table and Eq.(5), the explicit expressions for the sum of the infinite series can be written as
(17) 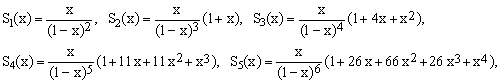
etc. Substituting for x specific values with |x| < 1, this leads to a number of particular infinite sums. In particular,
(18) 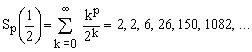 for p = 0, 1, 2, 3, 4, 5, ..., respectively (OEIS A076726). for p = 0, 1, 2, 3, 4, 5, ..., respectively (OEIS A076726).
For x = -1/2 one obtains
(19) 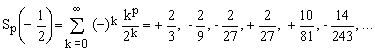 , again for p = 0, 1, 2, 3, 4, 5, ..., respectively. , again for p = 0, 1, 2, 3, 4, 5, ..., respectively.
For larger values of p the absolute values of this series become very large, while their signs continue to be quite unpredictable. For example, for p = 18 the result is about 2431084.21 while for p = 19 it is -6262402.20... The question of whether there is a finite or infinite number of sign changes in the sequence {Sp(-1/2)} looks like an unsolved problem of considerable complexity.
The denominators in (19) are integer powers of 3 and form the sequence OEIS A131137.
b) The polynomials Qp(x,n)
Since Qp(x,n) is a polynomial of degree p in both x and n, it can be written as
C-matrices for p = 1 to 5 and beyond
(25) The first five C-matrices are
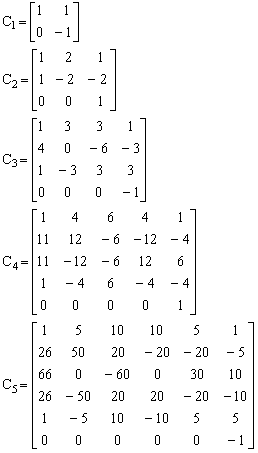 . .
For higher p values, use the Matlab program (caution: for p > 15 the results may go wrong due to overflow).
(20) 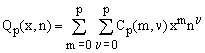 , ,
where Cp(m,ν) are numeric coefficients forming a square matrix of order (p+1) which we will call just C-matrix. Substituting Eq.(20) into Eq.(13) and comparing the coefficients, one obtains the following recurrence formula for the elements of the C-matrices:
(21) 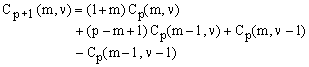 , ,
which, combined with the start-up coefficients given by Eq.(10),
(22) 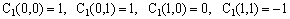 , ,
and with the rule that Cp(m,ν) = 0 whenever m and/or ν is either negative or greater than p, permits the determination of the C-matrices to any desired order.
In the C-matrices shown on the right the row index is m (i.e., the power of x) and the column index is ν (i.e., the power of n). In both cases, the numbering starts from 0. Thus, for example, Q2(x,n) can be written either as
(23a) 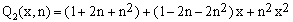
or as
(23b) 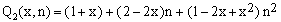 . .
Consequently, using the second form
(24) 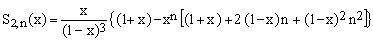 . .
Like the cp,k coefficients of the Pp(x) polynomials (Eq.16), the Cp(m,ν) satisfy a number of relations which are also easy to prove by recursion directly from Eqs.(21-22). Thus the sum of any column except the first one is null, the first row evaluates to (1+n)^p, the last row evaluates to (-xn)^p and, for m < p,
(26) 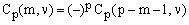 . .
IV. Alternative recurrences
It is relatively easy to find a direct recurrence for Sp,n(x).
Starting directly from the definition, one can proceed as follows:
(27) 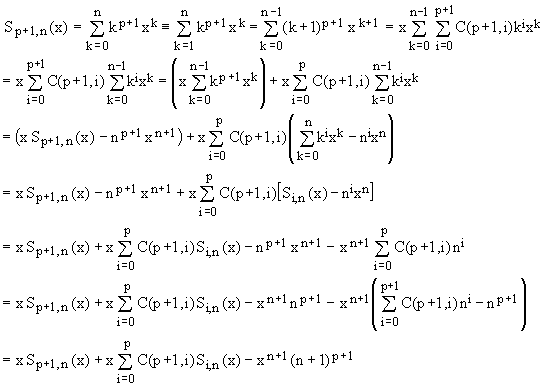 , ,
where C(n,m) is used to denote the binomial coefficients. This amounts to a direct recurrence for Sp,n(x)
(28) 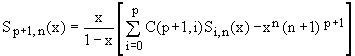 . .
Assuming |x| < 1 in order to guarantee convergence, and taking the limit of Eq.(28) for large n, it simplifies to a direct recurrence for the infinite series Sp(x) which makes evaluation of sequences like that in (19) relatively straightforward.
(29) 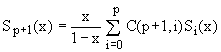 . .
The direct recurrences are often numerically more comfortable to use than tabulated polynomial expressions.
It is also clear that assuming the functional form of Eq.(4), one could easily work out direct recurrences for the polynomial values Pp(x) and Qp(x,n), without passing through their coefficients, but that is not the goal of this essay.
V. Special cases of finite sums
Using Eq.(4) and the known expressions for Pp(x) and Qp(x,n) one can now easily derive a number of notable finite-sum identities. For completeness sake, we list here also the results for p = 0 as given by Eq.(2).
a) Special cases for x = -1 (respectively, OEIS A059841, A130472, A089594, A232599)
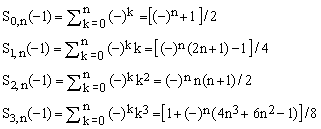 . .
b) Special cases for x = 2 (respectively, OEIS A232733, A036799, A036800, A036827)
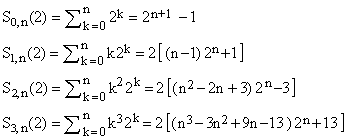 . .
c) Special cases for x = -2 (respectively, OEIS A077925, A232600, A232601, A232602)
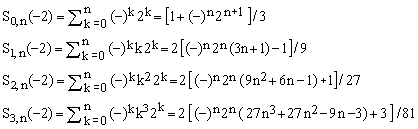 . .
d) Special cases for x = 1/2 (multiplied by 2 n, respectively, OEIS A000225, A000295, A047520, A213575)
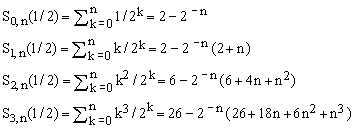 . .
e) Special cases for x = -1/2 (multiplied by 2 n, respectively, OEIS A001045, A053088, A232603, A232604)
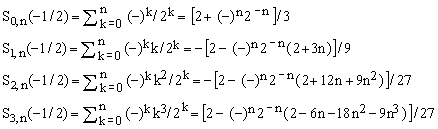 . .
|