Introduction

Let us suppose that a quantum system can be adequately described within the framework of an N-dimensional Hilbert space H and denote as L the linear vector space of all NxN linear operators on H (the space L is usually referred to as the Liouville space associated with H). In this Note we will show that:

• There exist in L triads {J_x,J_y,J_z} of traceless hermitian operators
  which satisfy the same commutator relations as the infinitesimal generators of the group SO3 of 3D rotations.
• All elements of L can be obtained from any two operators of any such triad by means of algebraic operations.

While proving these assertions, we will re-discover the standard angular momentum and spin algebra in the form it is used in applied particle, atomic and molecular physics, with a particular accent on nuclear magnetic resonance (NMR) and electron spin resonance (ESR).

Construction of the generators

(--A--) We choose an arbitrary orthonormal basis {B} in H
(--B--) and denote its elements as |m), with m being a half-integer label assuming the N values

    (1)    m = -S, -S+1, ... , S-1, S   where   S = (N-1)/2.

(--C--) We define three linear operators J_z , J⁺ and J^- in H by setting

    (2)    J_z|m) = z_m |m),    J⁺|m) = u_m |m+1),  and    J^-|m+1) = d_m |m),

where z_m , u_m and d_m are some complex coefficients whose values will be determined by imposing additional requirements on the operators. So far, the only conditions which need to be imposed are

    (3)   u_S = 0  and  d_-(S+1) = 0.

These requirements stem from the elementary fact that there are no base vectors |S+1) and |-S-1).

(--D--) We will also use the derived operators

    (4)   J_x = (J⁺ + J^-)/2   and   J_y = (J⁺ + J^-)/2j

and we shall require J_x , J_y and J_z to be hermitian. It is easily seen that to satisfy this requirement

    (5a)   z_m must be real numbers and
    (5b)   d_m = u_m*.

The latter condition implies also that J⁺ and J^- are hermitian conjugates of each other.

(--E--) Next we impose the condition that the operators J_x, J_y and J_z should obey the same commutation relations as the infinitesimal generators of the 3D rotation group O₃:

    (6)   [J_a , J_b] = je_abc J_c ,

where square brackets denote the commutator (i.e., [Q,P]=QP-PQ), a,b,c are indices selected from the set {x,y,z}, and e_abc is the anti-symmetric tensor whose only non-zero elements are:

    (7)   e_xyz = e_yzx = e_zxy = 1   and  e_yxz = e_xzy = e_zyx = -1.

The reader can easily verify that, expressed in terms of J_z , J⁺ and J^-, conditions (6) are equivalent to

    (8)   [J_z,J^±] = ±J^±   and   [J⁺,J^-] = 2J_z.

Relations (6) and (8), provided they can be satisfied by a suitable choice of coefficients (5), reveal the possibility of making L a representation of the 3D-rotation group, regardless of the dimension N of the underlying Hilbert space H.

The relations, together with equation (4), indicate also that any pair of operators chosen from the set [J_x, J_y, J_z, J⁺, J^-] can be used to generate the others.

(--F--) Another requirement we shall impose before determining the coefficients (5) is that J_z be traceless. The reason is that J_x and J_y are traceless by definition (Eqs.2,4) and symmetry transformations of any kind, when applied to linear operators, should not change their traces. Consequently, if J_z had a non-zero trace it would be impossible to obtain it from J_x and/or J_y by means of a rotation and the operators {J_x, J_y, J_z} could never form a representation of O₃.

(--G--) Let us now see whether it is really possible to satisfy the requirements (E,F).

Substituting Eqs.(2) into Eqs.(8), one obtains

    (9a)   (z_m+1-z_m) u_m = u_m ,     (z_m-z_m+1) d_m = -d_m ,
    (9b)   d_m-1u_m-1 - d_mu_m = 2z_m.

To satisfy conditions (9a), it is enough to set z_m = m+c, where c is a constant. Considering that, according to (F), the trace of J_z should be zero, we have c = 0 and therefore z_m = m.

Condition (9b) can be simplified using Eq.(5b), becoming

    (10)   |u_m|² = |u_m-1|² - 2z_m = |u_m-1|² - 2m.

This is a recurrence relation for the moduli of u_m which leaves their complex arguments (phases) completely unconstrained. For simplicity, we will look for real and non-negative u_m, but we should remember the existence of these extra degrees of freedom. Notice also that when u_m are non-negative real numbers then, according to Eq.(5b), so are the d_m. Eq.(10) can be now rewritten as

    (11)   κ_m = κ_m-1- 2m, where κ_m = u_m² and, according to Eq.(3), κ_S = 0.

The recurrence has a simple closed solution. Realizing that κ_m must be a quadratic expression in m, set κ_m = aκ²+bκ+c and then apply all the conditions to determine the coefficients a, b and c. The result is κ_m = S(S+1)-m(m+1), which means that choosing

    (12)   

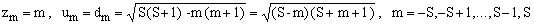
for the numerical coefficients in Eqs.(2), the operators {J_x, J_y, J_z} and J⁺, J^- satisfy all the the imposed conditions.

Those used to deal with angular momentum and/or spins are of course well acquainted with all the above formulae, including the form of the coefficients shown in Eqs.(12). What is new in the above exposition is the fact that we are not discussing any particular physical system. So far, in fact, we have just imposed a number of conditions and showed that, regardless of the dimension N of the Hilbert space H, it was possible to pick up a triad of operators on H (elements of L) which satisfy them. We have not yet proved anything beyond the existence of such a triad.

Proof of completeness

We will now prove the following

Theorem: The operators J⁺ and J^- generate the whole space L.

For a moment, let us continue to use the chosen orthonormal basis {B} in H. We shall use the base vectors of {B} to define the following generalized projection operators:

    (13)   T_km = |k)(m|.

Any linear operator Q can be written as a linear combination the generalized projection operators. In fact, considering that the only nonzero matrix element of T_km in {B} is the one corresponding to row k and column m and that its value is 1, we have

    (14)   

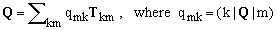
are the matrix coefficients of Q in {B}. Consequently, should we prove that any generalized projection operator can be expressed algebraically by means of our generators, the Theorem would be proved as well.

To prove that this is indeed so, we will first show that

    (15)   ,

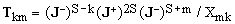where X_mk are some non-zero coefficients.

Consider the following statements, each of which is an direct consequence of the requirements imposed in the previous Section:
a) (J^- )^S+m|p) is null unless p ≥ m, in which case it is proportional to |r), where r = -S-m+p,
b) (J⁺)^2S   |r) is null unless r = -S, in which case it is proportional to |S), and
c) (J^- )^S-k |S) is proportional to |k).

Together, the three statements imply that the operator corresponding to the composition of the corresponding steps nulls all base vectors |p) with the only exception of |m), for which the result is proportional to |k). Consequently,

    (16)   ,

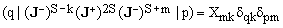which is equivalent to Eq.(15).

It is also relatively easy to determine explicitly the values of the X-coefficients. Explicit evaluation leads to

    (17a)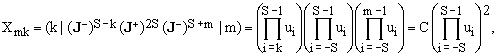   

    (17b)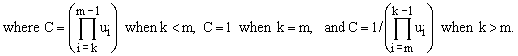   

Using the explicit expression for u_i, Eq.(12), one obtains

    (17c)   ,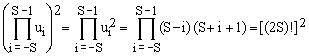

as well as the following expression for C which turns out to apply to all three cases of Eq.(17b):

    (17d)   .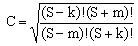

Combining all these partial results, we have

    (18)   .

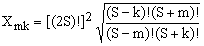We can thus conclude this Section by an explicit formula which expresses any operator on H (i.e., any element of L) in terms of just two operators, J⁺ and J^-:

    (19)   .

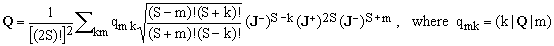Considering Eq.(4), it is evident that Q could be rewritten also in terms of J_x and J_y. On the other hand, there is no explicit need for J_z in this context since, according to the second of Eqs.(8), J_z is itself a function of J⁺ and J^-.

Physical considerations

So far our discussion was purely mathematical and for the most part consisted in showing that it is possible to find triads of operators

    (20)    J ≡ {J_x, J_y, J_z} or, equivalently, J' ≡ {J⁺, J^-, J_z}

which are homomorphic with the infinitesimal generators of the group of 3D-rotations and from which it is possible to generate every operator on H (i.e., element of L) by means of the algebraic operations of sum and product. This emerged from the rather artful way the triads were constructed, imposing a series of mathematical requirements which may appear intuitive to those who already have some knowledge of spin algebras but probably sound a bit arbitrary to everybody else.

It also emerged that there are many such triads. Choosing any orthonormal basis in H, one can construct a set of such triads. Withing each such set, there is exactly one triad for which all the z-, d- and u-coefficients are real (we can call it the canonical triad). The other triads differ from it by arbitrary complex-unity 'phases' applied to the u-coefficients (the d-coefficients then follow from Eq.5b).

What does all this mean from the point of view of actual physical systems which are being described within the quantum-mechanical framework of an N-dimensional Hilbert space? A curt and rude answer to this question could be 'nothing, unless the physical system has some special properties'.

Every physical system is associated with a hermitian operator E on H, called Hamiltonian, which defines the free-evolution of the system when left to itself. There exists in H at least one orthonormal base which diagonalizes E (in the absence of degeneracy, such an eigenbase of E is unique). To each eigenbase then corresponds a canonical triad J which we will call an eigentriad of the system (again, when there is no degeneracy, the eigentriad is unique). According to Eq.(19), E can be written in terms of the eigentriad J's as

    (21)   

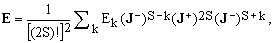
where E_k are the eigenvalues of E. Identity (21) expresses E as a 4S-degree polynomial of the eigentriad operators.

Being completely general, Eq.(21) is equivalent to expressing E by means of transition operators between eigenstates and does not offer any special advantages. The situation changes when the dynamic structure of the physical system is such that its Hamiltonian E can be written in terms of an eigentriad of operators using only very low-order polynomials. Any simplification of Eq.(21) in fact justifies the use of the spin-like generators and when the simplification is massive, the approach becomes a natural way of describing the system. Whether this happens or not is a physical question which can only be answered by suitable experiments.

Since the operators of J are hermitian, they correspond to some observables of the system. It often happens that in real systems the observables in question are true 3D-vector components to which one can apply classical 3D rotations. When this is true and the situation described in the previous paragraph applies as well, we have a simple spin system such as a particle with intrinsic spin or a rotating solid body. Again, whether this is the case or not can only be determined experimentally.

In some systems (such as subatomic particles) the observables corresponding to eigentriads can not be interpreted as 3D vectors but, nevertheless, simplify expression (21). In such cases the system has pseudo-spin properties (such as color and charm). These can be further classified according to the experimentally determined symmetry group of which the eigentriad observables might be a representation.

In a sense, the choice of a triad of spin-operators as generators of L is similar to the choice of a system of spherical coordinates in classical mechanics: it may be very useful in some cases, while being counter-productive in others. By themselves, spherical coordinates are universal and - like all coordinate systems - can be used to describe any physical object. Their use, however, becomes really convenient only when the described system has a sufficiently high symmetry.

In physics classes, it is customary to introduce angular-momentum and spin algebras starting from physical concepts (angular momentum, spin) and adapting the math to the problem at hand. Such an approach often masks the demarcation line between the math and the physical application. This can confuse the student and make him miss those math features which are universally applicable far beyond the boundaries of the specific physical problem.

Some spin-operator identities

From the explicit expressions for the z-, u-, and d-coefficients it follows that, for any base vector |m),

    (22)   .

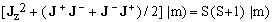Consequently,

    (23)   ,

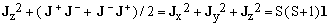where 1 is the identity operator. When the triad J is interpreted as a 3D-vector operator, Eq.(23) says that the length of the vector is constant and its square equals S(S+1). Keep in mind, however, that the equation would hold even if J could not be interpreted as a vector.

Another universal identity arises by setting Q = 1 in Eq.(19):

    (24)   

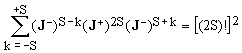
(in order to improve readability, the identity operator has been dropped). Special cases of Eq.(24):

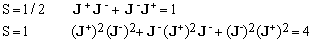
Eq.(24) is a special case of the following identity obtained by setting Q = J_z^p in Eq.(19), for integer, non-negative p:

    (25)   .

Special cases of Eq.(25) for p=1:

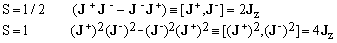
The first of these identities holds for any S (see Eq.8), while the second one is specific for S=1.