1. Introduction: free form expression for generic rotations

Let u be a unit-length vector (called also a versor) which defines a direction in space. Let, moreover, m be an arbitrary position vector. When m is rotated by an angle α around an axis which passes through the origin of coordinates and whose direction is given by u, the rotated vector m' is given by

(1)   ,

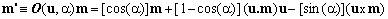where (a.b) denotes the scalar (inner) product of two vectors, (a x b) their vector product and O(u,α) is the rotation operator.

The above formula is expressed in a free form, meaning that it is independent of any particular coordinate system.

2. Application to NMR RF pulses

We now choose the standard NMR coordinate system in which the Z-axis is aligned in the direction of the main (static) magnetic field B0 and, within the perpendicular XY plane, the x-axis is defined by the direction of the rotating RF field B1 when the RF phase is set equal to 0°.

Elementary NMR theory says that a non-selective NMR RF pulse with carrier frequency reasonably close to resonance acts on the nuclear magnetization vector m of any sample component by making it to rotate around a versor u lying in the XY-plane by a nutation angle α (any longitudinal component of u, even if present, is rather ineffective and can be neglected). In the chosen coordinate system, the versor u takes on the form

(2)   ,

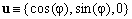where φ is the pulse phase. Substituting Eq.(2) in Eq.(1) and using matrix notation, it follows that the effect of a non-selective on-resonance RF pulse with phase φ and nutation angle α on a nuclear magnetization vector m can be described by multiplying m by the following matrix (tensor) P(α,φ):

(3a)   .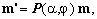

         .

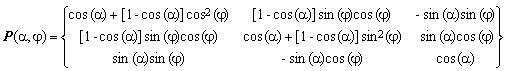Explicitly, using the vector components of m, the application of an RF pulse corresponds to the operation

(3b)   .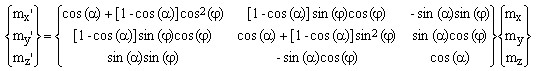

Equations (3) do not take into account any quantum effects present in coupled spin systems but, like Bloch equations, permit a rather good simulation of RF pulse effects whenever Zeeman interaction is dominant and sufficient to account for the observed phenomena. Typically, this includes MRI and most low-resolution NMR situations.

The reader can easily verify that RF pulses with phase φ = 0° (or x-labelled) correspond to simple rotations around the X-axis, while those with phase φ = 90° (or y-labelled) define rotations around the Y-axis. It is also evident that the pulse matrix P(α,φ) is orthogonal and its trace is 1+2cos(α), independent of the versor direction. These are general characteristics of all rotation matrices, a topic which exceeds the scope of this Note and will be discussed elsewhere.

3. Evolution during delays between pulses

In an NMR sequence, RF pulses are usually interspersed with delay intervals during which the magnetization evolves, within the current approximation, according to the phenomenological Bloch equations which may be written as:

(4)   .

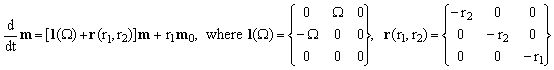are, respectively, the infinitesimal Larmor precession operator and the relaxation rate matrix. The following properties of the considered magnetization component m are used:

   Ω is the resonance offset 
   r₁ = 1/T₁ is the longitudinal relaxation rate (inverse of the relaxation time T₁),
   r₂ = 1/T₂ is the perpendicular relaxation rate (inverse of the relaxation time T₂), and
   m₀ = {0, 0, m₀}, where m₀ is the equilibrium value of the magnetization component.

Starting with an arbitrary state m_i of the magnetization component and allowing it to evolve for a period of duration Δ, its final state m_f, determined by integration of the first-order differential equation (4), can be written as:

(5a)   .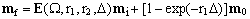

where E is the free-evolution matrix operator which, in turn, is a product of the diagonal relaxation matrix R and the Larmor matrix L:

(5b)   .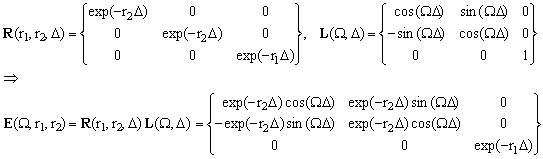

Notice that, due to the presence of equilibrium magnetization in Eqs.(4) and (5a), the magnetization evolution is inhomogeneous and can not be expressed by means of a single linear matrix operator.

4. Practical uses of the equations

Given any pulse sequence composed of non-selective on-resonance RF pulses, each with a specified RF phase and nutation angle, preceded/followed by free evolution intervals of specified duration, Equations (3) and (5) allow us to easily follow the evolution of any magnetization component during the sequence from its given initial state to whatever is its final state.

What complicates things in practice, apart from the accepted approximations, is the fact that, in a real sample measured on a real instrument, all the involved parameters are subject to statistical distributions: Thus

   - RF pulse nutation angles and phases often have a significant spread of values due to B1 inhomogeneity,
   - resonance offsets may be spread due to intrinsic field inhomogeneity or imposed field gradients, and
   - relaxation values may have more or less wide distributions due to sample heterogeneity.

The effects of such distributions on the performance of a pulse sequence and on its experimental results are often difficult to assess. In many cases the outcomes are remarkably insensitive to some of these factors, while in others they give rise to severe artifacts. A phenomenological assessment of such aspects requires a simulation involving suitable hypotheses about the distributions of the involved parameters and an integration of the evolution equations over all involved magnetization components, each with its own evolution path defined by Eqs.(3) and (5).

An aspect of Eqs.(1) and (3) which might lead to confusion is the sign of the nutation angle. The equations shown above assume a clockwise rotation for positive angles, a choice which has to do more with NMR conventions than with math (in fact, it has been opposite in the first draft of this Note). When applying a 90-degrees pulse with phase 0 (rotation around x-axis) to a relaxed magnetization vector {0,0,1}, the latter becomes {0,1,0}. With the receiver-phase convention assigning the in-phase (real) signal u(t) to the y-component of m(t) and the out-of-phase (imaginary) signal v(t) to its x-component, this amounts to a signal with positive real part and null imaginary part. The present choice of the nutation angle sign, combined with the receiver-signal assignements

(6)   u = m_y, v = m_x

therefore matches standard textbook conventions.

5. Matlab utilities

Those who are familiar with MATLAB and wish to simulate the effects of pulse sequences on magnetization vectors may download and use two simple MATLAB functions, pulse.m and delay.m, which embody Eqs.(3) and (5). In subsequent Notes the author will use these functions in MATLAB programs designed to simulate and analyze various artifacts in classical LR-NMR sequences.