Introduction

Barely two months have passed since the publication of my Review (hence just R) on the Approximations of Ellipse Perimeters and I already feel compelled to amend it. There are two specific reasons for this:

(1) I have concluded R with the following challenge:

Those who wish to pursue this topic further should look for an efficient formula using only the four algebraic operations (if possible, avoiding even square-root) with a maximum error below 10 ppm. If would be also nice if such a formula were exact for both the circle (y=1) and the degenerate flat ellipse (y=0).

Writing those words, I certainly did not expect that in less than one month David W.Cantrell would come up with an approximation that meets all those criteria and has the maximum relative error of just 5.2 ppm !!!

(2) David, Gérard P.Michon and I have exchanged several e-mails which clarified an issue of priority, plus some minor points which are worth mentioning.

The new approximation

(C7) Cantrell 2006

The new approximation is exact for both y = 1 (circle) and y = 0 (degenerate, flat ellipse) and has three zero crossings, i.e., points at which S'(a,b) = S(a,b). According to the classification of the original Review, it therefore belongs to category C and becomes its seventh and most successful member. The new formulae, originating from an artful combination of arithmetic, geometric and harmonic means, are:

(C7)   ,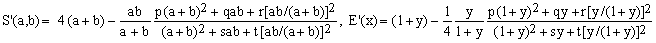

where p, q, r, s and t are numeric parameters. For the formula to be exact at y=0, r must equal 4[(4-π)(4s+t+16)-(4p+q)], leaving four parameters to be adjusted so as to minimize the maximum relative error. The resulting optimal values are p = 3.982901, q = 66.71674, s = 18.31287, t = 23.39728 and r = 56.2007. Notice that, due to the repetition of many factors occurring in Eqs.(C7), the evaluation of the formula is computationally quite efficient.

Cantrell shows that there is an extended lower-dimensional region in the space of the parameters {p,q,s,t} in which the maximum relative error remains close to its best value of 5.2 ppm. This is reminiscent of fitting transcendental functions by high-order polynomials where one also finds extensive regions of parameter combinations within which the fits remain quite satisfactory.

The error curve of the new approximation is shown in blue color in the Figure below. For comparison, the Figure shows the error curves for five most successful approximations found so far (excluding the Padé combinations discussed in R).

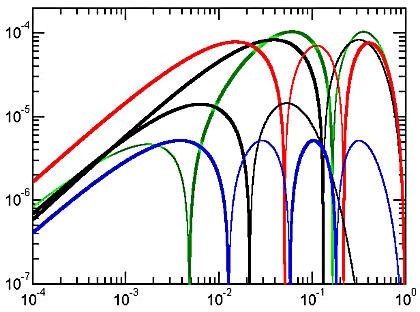
Error curves for the best approximations with exact extremes 

In order of decreasing maximum relative error, the approximations are: (R:C3, green) Rivera II, (R:C4, black) Cantrell I, (R:C5, red) Sykora, (R:C6, black) Cantrell-Ramanujan, and (C7, blue) Cantrell 2006. The thin lobes of each curve correspond to negative deviations with S'(a,b)<=S(a,b) and the thick ones to non-negative deviations. Approximations (R:C5) and (C7) are the only ones containing only basic arithmetic operations.
 

Various comments

The following comments stem from discussions between me and David Cantrell, whom I thank for his help and friendly advice.

Priority claims for (R:E5)

When writing my first article on ellipse perimeters, I was convinced that (R:E5) was quite original. Soon after the article went online, however, I have found out that the formula matches the first term of D.F.Rivera's approximation (R:C3). I have therefore amended the article with a note to that effect and, in the Review, coined the term Sykora-Rivera approximation. Then, reading the article and the Review, David Cantrell realized that an earlier expression of his which he called particularly fruitful, though written differently, is identical to mine and Rivera's. Mentioning the fact to me, he added:

I doubt that I am the first person to have suggested using (R:E5) to approximate the perimeter of an ellipse.
It's such a simple approximation that it was probably suggested long ago by someone else. But who?

I therefore suggest that (R:E5) be henceforth called Cantrell's Particularly Fruitful approximation.

Optimization of (R:C5)

This formula originates from my first article where it has been cast in a more general form (Eqs.9-10) containing two adjustable parameters whose optimal values, λ = -0.50079... and μ = 3.1524..., give maximum relative error of 76 ppm. Intrigued by the fact that these optimal values are so close to the esthetically pleasing λ = -1/2 and μ = π, I have opted for the latter despite the fact that this leads to a slightly larger error (78.5 ppm). Since David disagrees with such numerological mysticism, I list here the optimized form of (R:C5), leaving it to the readers to decide whether they like it more or not:

(R:C5, optimal)  ,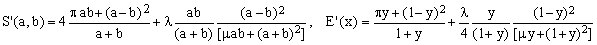

with the optimal values of λ and μ given above.

Matters of numeric efficiency

Next goal

The only possible way to conclude this Addendum is by re-iterating the original challenge with more stringent numeric limits:

Those who wish to pursue this topic further should look for an efficient formula using only the four algebraic operations (if possible, avoiding even square-root) with a maximum error smaller than 1 ppm. In addition, the formula should be exact for both the circle (y=1) and the degenerate flat ellipse (y=0).